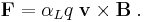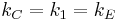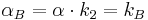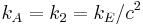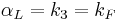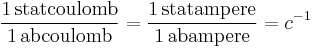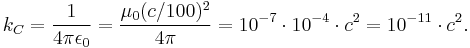Centimetre–gram–second system of units
The centimetre–gram–second system (abbreviated CGS or cgs) is a metric system of physical units based on centimetre as the unit of length, gram as a unit of mass, and second as a unit of time. All CGS mechanical units are unambiguously derived from these three base units, but there are several different ways of extending the CGS system to cover electromagnetism.
The CGS system has been largely supplanted by the MKS system, based on metre, kilogram, and second. MKS was in turn extended and replaced by the International System of Units (SI). The latter adopts the three base units of MKS, plus the ampere, mole, candela and kelvin. In many fields of science and engineering, SI is the only system of units in use. However, there remain certain subfields where CGS is prevalent.
In measurements of purely mechanical systems (involving units of length, mass, force, energy, pressure, and so on), the differences between CGS and SI are straightforward and rather trivial; the unit-conversion factors are all powers of 10 arising from the relations 100 cm = 1 m and 1000 g = 1 kg. For example, the CGS derived unit of force is the dyne, equal to 1 g·cm/s2, while the SI derived unit of force is the newton, 1 kg·m/s2. Thus it is straightforward to show that 1 dyne=10−5 newtons.
On the other hand, in measurements of electromagnetic phenomena (involving units of charge, electric and magnetic fields, voltage, and so on), converting between CGS and SI is much more subtle and involved. In fact, formulas for physical laws of electromagnetism (such as Maxwell's equations) need to be adjusted depending on what system of units one uses. This is because there is no one-to-one correspondence between electromagnetic units in SI and those in CGS, as is the case for mechanical units. Furthermore, within CGS, there are several plausible choices of electromagnetic units, leading to different unit "sub-systems", including Gaussian, "ESU", "EMU", and Heaviside–Lorentz. Among these choices, Gaussian units are the most common today, and in fact the phrase "CGS units" is often used to refer specifically to CGS-Gaussian units.
History
The CGS system goes back to a proposal made in 1832 by the German mathematician Carl Friedrich Gauss.[1] In 1874, it was extended by the British physicists James Clerk Maxwell and William Thomson with a set of electromagnetic units.
The values (by order of magnitude) of many CGS units turned out to be inconvenient for practical purposes. For example, many everyday length measurements yield hundreds or thousands of centimetres, such as those of human height and sizes of rooms and buildings. Thus the CGS system never gained wide general use outside the field of electrodynamics and laboratory science. Starting in the 1880s, and more significantly by the mid-20th century, CGS was gradually superseded internationally by the MKS (metre–kilogram–second) system, which in turn became the modern SI standard.
From the international adoption of the MKS standard in the 1940s and the SI standard in the 1960s, the technical use of CGS units has gradually declined worldwide, in the United States more slowly than elsewhere. CGS units are today no longer accepted by the house styles of most scientific journals, textbook publishers, or standards bodies, although they are commonly used in astronomical journals such as the Astrophysical Journal. CGS units are still occasionally encountered in technical literature, especially in the United States in the fields of material science, electrodynamics and astronomy. The continued usage of CGS units is most prevalent in magnetism and related fields, as the primary MKS unit, the tesla, is inconvenienently large, leading to the continued common use of the gauss, the CGS equivalent.
The units gram and centimetre remain useful as prefixed units within the SI system, especially for instructional physics and chemistry experiments, where they match the small scale of table-top setups. However, where derived units are needed, the SI ones are generally used and taught instead of the CGS ones today. For example, a physics lab course might ask students to record lengths in centimeters, and masses in grams, but force (a derived unit) in newtons, a usage consistent with the SI system.
Definition of CGS units in mechanics
In mechanics, the CGS and SI systems of units are built in an identical way. The two systems differ only in the scale of two out of the three base units (centimetre versus metre and gram versus kilogram, respectively), while the third unit (second as the unit of time) is the same in both systems.
There is a one-to-one correspondence between the base units of mechanics in CGS and SI, and the laws of mechanics are not affected by the choice of units. The definitions of all derived units in terms of the three base units are therefore the same in both systems, and there is an unambiguous one-to-one correspondence of derived units:
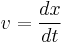 (definition of velocity)
(definition of velocity)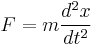 (Newton's second law of motion)
(Newton's second law of motion)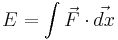 (energy defined in terms of work)
(energy defined in terms of work)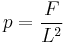 (pressure defined as force per unit area)
(pressure defined as force per unit area)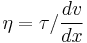 (dynamic viscosity defined as shear stress per unit velocity gradient).
(dynamic viscosity defined as shear stress per unit velocity gradient).
Thus, for example, the CGS unit of pressure, barye, is related to the CGS base units of length, mass, and time in the same way as the SI unit of pressure, pascal, is related to the SI base units of length, mass, and time:
- 1 unit of pressure = 1 unit of force/(1 unit of length)2 = 1 unit of mass/(1 unit of length·(1 unit of time)2)
- 1 Ba = 1 g/(cm·s2)
- 1 Pa = 1 kg/(m·s2).
Expressing a CGS derived unit in terms of the SI base units, or vice versa, requires combining the scale factors that relate the two systems:
- 1 Ba = 1 g/(cm·s2) = 10-3 kg/(10-2 m·s2) = 10-1 kg/(m·s2) = 10-1 Pa.
Definitions and conversion factors of CGS units in mechanics
| Quantity | Symbol | CGS unit | CGS unit abbreviation |
Definition | Equivalent in SI units |
|---|---|---|---|---|---|
| length, position | L, x | centimetre | cm | 1/100 of metre | = 10−2 m |
| mass | m | gram | g | 1/1000 of kilogram | = 10−3 kg |
| time | t | second | s | 1 second | = 1 s |
| velocity | v | centimetre per second | cm/s | cm/s | = 10−2 m/s |
| acceleration | a | gal | Gal | cm/s2 | = 10−2 m/s2 |
| force | F | dyne | dyn | g·cm/s2 | = 10−5 N |
| energy | E | erg | erg | g·cm2/s2 | = 10−7 J |
| power | P | erg per second | erg/s | g·cm2/s3 | = 10−7 W |
| pressure | p | barye | Ba | g/(cm·s2) | = 10-1 Pa |
| dynamic viscosity | μ | poise | P | g/(cm·s) | = 10-1 Pa·s |
| wavenumber | k | kayser | cm−1 | cm−1 | = 100 m−1 |
Derivation of CGS units in electromagnetism
CGS approach to electromagnetic units
The conversion factors relating electromagnetic units in the CGS and SI systems are much more involved – so much so that formulas for physical laws of electromagnetism are adjusted depending on what system of units one uses. This illustrates the fundamental difference in the ways the two systems are built:
- In SI, the unit of electric current is chosen[2] to be 1 ampere (A). It is a base unit of the SI system, along with meter, kilogram, and second. The ampere is not dimensionally equivalent to any combination of other base units, so electromagnetic laws written in SI require an additional constant of proportionality (see Vacuum permittivity) to bridge electromagnetic units to kinematic units. All other electric and magnetic units are derived from these four base units using the most basic common definitions: for example, electric charge q is defined as current I multiplied by time t,
-
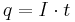 ,
,
- therefore unit of electric charge, coulomb (C), is defined as 1 C = 1 A·s.
- CGS system avoids introducing new base units and instead derives all electric and magnetic units from centimeter, gram, and second based on the physics laws that relate electromagnetic phenomena to mechanics.
Alternate derivations of CGS units in electromagnetism
Electromagnetic relationships to length, time and mass may be derived by several equally appealing methods. Two of them rely on the forces observed on charges. Two fundamental laws relate (independently of each other) the electric charge or its rate of change (electric current) to a mechanical quantity such as force. They can be written[3] in system-independent form as follows:
- The first is Coulomb's law,
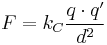 , which describes the electrostatic force F between electric charges
, which describes the electrostatic force F between electric charges  and
and 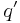 , separated by distance d. Here
, separated by distance d. Here 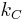 is a constant which depends on how exactly the unit of charge is derived from the CGS base units.
is a constant which depends on how exactly the unit of charge is derived from the CGS base units.
- The second is Ampère's force law,
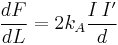 , which describes the magnetic force F per unit length L between currents I and I' flowing in two straight parallel wires of infinite length, separated by a distance d that is much greater than the wire diameters. Since
, which describes the magnetic force F per unit length L between currents I and I' flowing in two straight parallel wires of infinite length, separated by a distance d that is much greater than the wire diameters. Since 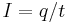 and
and 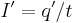 , the constant
, the constant 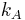 also depends on how the unit of charge is derived from the CGS base units.
also depends on how the unit of charge is derived from the CGS base units.
Maxwell's theory of electromagnetism relates these two laws to each other. It states that the ratio of proportionality constants 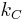 and
and 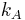 must obey
must obey 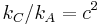 , where c is the speed of light in vacuum. Therefore, if one derives the unit of charge from the Coulomb's law by setting
, where c is the speed of light in vacuum. Therefore, if one derives the unit of charge from the Coulomb's law by setting 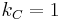 , it is obvious that the Ampère's force law will contain a prefactor
, it is obvious that the Ampère's force law will contain a prefactor 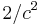 . Alternatively, deriving the unit of current, and therefore the unit of charge, from the Ampère's force law by setting
. Alternatively, deriving the unit of current, and therefore the unit of charge, from the Ampère's force law by setting 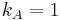 or
or 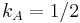 , will lead to a constant prefactor in the Coulomb's law.
, will lead to a constant prefactor in the Coulomb's law.
Indeed, both of these mutually-exclusive approaches have been practiced by the users of CGS system, leading to the two independent and mutually-exclusive branches of CGS, described in the subsections below. However, the freedom of choice in deriving electromagnetic units from the units of length, mass, and time is not limited to the definition of charge. While the electric field can be related to the work performed by it on a moving electric charge, the magnetic force is always perpendicular to the velocity of the moving charge, and thus the work performed by the magnetic field on any charge is always zero. This leads to a choice between two laws of magnetism, each relating magnetic field to mechanical quantities and electric charge:
- The first law describes the Lorentz force produced by a magnetic field B on a charge q moving with velocity v:
- The second describes the creation of a static magnetic field B by an electric current I of finite length dl at a point displaced by a vector r, known as Biot-Savart law:
-
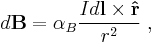 where r and
where r and 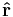 are the length and the unit vector in the direction of vector r.
are the length and the unit vector in the direction of vector r.
These two laws can be used to derive Ampère's force law above, resulting in the relationship: 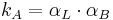 . Therefore, if the unit of charge is based on the Ampère's force law such that
. Therefore, if the unit of charge is based on the Ampère's force law such that 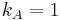 , it is natural to derive the unit of magnetic field by setting
, it is natural to derive the unit of magnetic field by setting 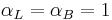 . However, if it is not the case, a choice has to be made as to which of the two laws above is a more convenient basis for deriving the unit of magnetic field.
. However, if it is not the case, a choice has to be made as to which of the two laws above is a more convenient basis for deriving the unit of magnetic field.
Furthermore, if we wish to describe the electric displacement field D and the magnetic field H in a medium other than vacuum, we need to also define the constants ε0 and μ0, which are the vacuum permittivity and permeability, respectively. Then we have[3] (generally) 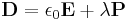 and
and 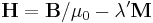 , where P and M are polarization density and magnetization vectors. The factors λ and λ′ are rationalization constants, which are usually chosen to be
, where P and M are polarization density and magnetization vectors. The factors λ and λ′ are rationalization constants, which are usually chosen to be 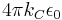 , a dimensionless quantity. If λ = λ′ = 1, the system is said to be "rationalized":[4] the laws for systems of spherical geometry contain factors of 4π (for example, point charges), those of cylindrical geometry – factors of 2π (for example, wires), and those of planar geometry contain no factors of π (for example, parallel-plate capacitors). However, the original CGS system used λ = λ′ = 4π, or, equivalently,
, a dimensionless quantity. If λ = λ′ = 1, the system is said to be "rationalized":[4] the laws for systems of spherical geometry contain factors of 4π (for example, point charges), those of cylindrical geometry – factors of 2π (for example, wires), and those of planar geometry contain no factors of π (for example, parallel-plate capacitors). However, the original CGS system used λ = λ′ = 4π, or, equivalently, 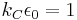 . Therefore, Gaussian, ESU, and EMU subsystems of CGS (described below) are not rationalized.
. Therefore, Gaussian, ESU, and EMU subsystems of CGS (described below) are not rationalized.
Various extensions of the CGS system to electromagnetism
The table below shows the values of the above constants used in some common CGS subsystems:
| system | 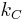 |
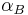 |
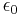 |
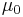 |
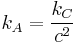 |
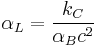 |
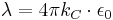 |
 |
|---|---|---|---|---|---|---|---|---|
| Electrostatic[3] CGS (ESU, esu, or stat-) |
1 | c−2 | 1 | c−2 | c−2 | 1 | 4π | 4π |
| Electromagnetic[3] CGS (EMU, emu, or ab-) |
c2 | 1 | c−2 | 1 | 1 | 1 | 4π | 4π |
| Gaussian[3] CGS | 1 | c−1 | 1 | 1 | c−2 | c−1 | 4π | 4π |
| Lorentz–Heaviside[3] CGS | 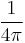 |
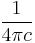 |
1 | 1 | 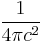 |
c−1 | 1 | 1 |
| SI | 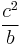 |
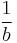 |
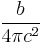 |
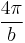 |
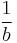 |
1 | 1 | 1 |
The constant b in SI system is a unit-based scaling factor defined as: 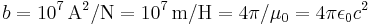 .
.
Also, note the following correspondence of the above constants to those in Jackson[3] and Leung:[5]
In system-independent form, Maxwell's equations in vacuum can be written as:[3][5]
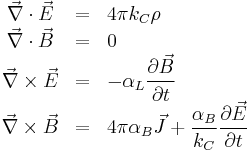
Note that of all these variants, only in Gaussian and Heaviside–Lorentz systems 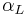 equals
equals 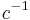 rather than 1. As a result, vectors
rather than 1. As a result, vectors 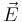 and
and 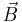 of an electromagnetic wave propagating in vacuum have the same units and are equal in magnitude in these two variants of CGS.
of an electromagnetic wave propagating in vacuum have the same units and are equal in magnitude in these two variants of CGS.
Electrostatic units (ESU)
In one variant of the CGS system, Electrostatic units (ESU), charge is defined via the force it exerts on other charges, and current is then defined as charge per time. It is done by setting the Coulomb force constant 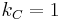 , so that Coulomb's law does not contain an explicit prefactor.
, so that Coulomb's law does not contain an explicit prefactor.
The ESU unit of charge, franklin (Fr), also known as statcoulomb or esu charge, is therefore defined as follows:[6]
two equal point charges spaced 1 centimetre apart are said to be of 1 franklin each if the electrostatic force between them is 1 dyne.
Therefore, in electrostatic CGS units, a franklin is equal to a centimetre times square root of dyne:
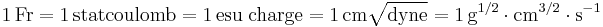 .
.
The unit of current is defined as:
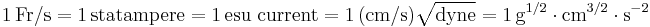 .
.
Dimensionally in the ESU CGS system, charge q is therefore equivalent to m1/2L3/2t−1. Neither charge nor current are therefore an independent dimension of physical quantity in ESU CGS. This reduction of units is an application of the Buckingham π theorem.
ESU notation
All electromagnetic units in ESU CGS system that do not have proper names are denoted by a corresponding SI name with an attached prefix "stat" or with a separate abbreviation "esu".[6]
Electromagnetic units (EMU)
In another variant of the CGS system, Electromagnetic units (EMU), current is defined via the force existing between two thin, parallel, infinitely long wires carrying it, and charge is then defined as current multiplied by time. (This approach was eventually used to define the SI unit of ampere as well). In the EMU CGS subsystem, is done by setting the Ampere force constant 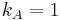 , so that Ampère's force law simply contains 2 as an explicit prefactor (this prefactor 2 is itself a result of integrating a more general formulation of Ampère's law over the length of the infinite wire).
, so that Ampère's force law simply contains 2 as an explicit prefactor (this prefactor 2 is itself a result of integrating a more general formulation of Ampère's law over the length of the infinite wire).
The EMU unit of current, biot (Bi), also known as abampere or emu current, is therefore defined as follows:[6]
The biot is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular cross-section, and placed one centimetre apart in vacuum, would produce between these conductors a force equal to two dynes per centimetre of length.
Therefore, in electromagnetic CGS units, a biot is equal to a square root of dyne:
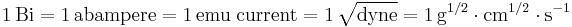 .
.
The unit of charge in CGS EMU is:
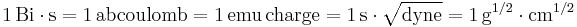 .
.
Dimensionally in the EMU CGS system, charge q is therefore equivalent to m1/2L1/2. Neither charge nor current are therefore an independent dimension of physical quantity in EMU CGS.
EMU notation
All electromagnetic units in EMU CGS system that do not have proper names are denoted by a corresponding SI name with an attached prefix "ab" or with a separate abbreviation "emu".[6]
Relations between ESU and EMU units
The ESU and EMU subsystems of CGS are connected by the fundamental relationship 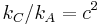 (see above), where c = 29,979,245,800 ≈ 3·1010 is the speed of light in vacuum in cm/s. Therefore, the ratio of the corresponding “primary″ electrical and magnetic units (e.g. current, charge, voltage, etc. – quantities proportional to those that enter directly into Coulomb's law or Ampère's force law) is equal either to c-1 or c:[6]
(see above), where c = 29,979,245,800 ≈ 3·1010 is the speed of light in vacuum in cm/s. Therefore, the ratio of the corresponding “primary″ electrical and magnetic units (e.g. current, charge, voltage, etc. – quantities proportional to those that enter directly into Coulomb's law or Ampère's force law) is equal either to c-1 or c:[6]
and
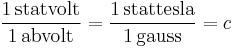 .
.
Units derived from these may have ratios equal to higher powers of c, for example:
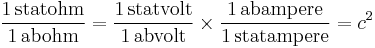 .
.
Other variants
There were at various points in time about half a dozen systems of electromagnetic units in use, most based on the CGS system.[7] These also include Gaussian units, and Heaviside–Lorentz units.
Further complicating matters is the fact that some physicists and engineers in the United States use hybrid units, such as volts per centimetre for electric field. In fact, this is essentially the same as the SI unit system, by the variant to translate all lengths used into cm, e.g. 1 m = 100 cm.
Electromagnetic units in various CGS systems
| Quantity | Symbol | SI unit | ESU unit | EMU unit | Gaussian unit |
|---|---|---|---|---|---|
| electric charge | q | 1 C | = (10−1 c) statC | = (10−1) abC | = (10−1 c) Fr |
| electric current | I | 1 A | = (10−1 c) statA | = (10−1) abA | = (10−1 c) Fr·s−1 |
| electric potential voltage |
φ V |
1 V | = (108 c−1) statV | = (108) abV | = (108 c−1) statV |
| electric field | E | 1 V/m | = (106 c−1) statV/cm | = (106) abV/cm | = (106 c−1) statV/cm |
| magnetic B field | B | 1 T | = (104 c−1) statT | = (104) G | = (104) G |
| magnetic H field | H | 1 A/m | = (4π 10−3 c) statA/cm | = (4π 10−3) Oe | = (4π 10−3) Oe |
| magnetic dipole moment | μ | 1 A·m² | = (103 c) statA·cm² | = (103) abA·cm² | = (103) erg/G |
| magnetic flux | Φm | 1 Wb | = (108 c−1) statT·cm² | = (108) Mw | = (108) G·cm² |
| resistance | R | 1 Ω | = (109 c−2) s/cm | = (109) abΩ | = (109 c−2) s/cm |
| resistivity | ρ | 1 Ω·m | = (1011 c−2) s | = (1011) abΩ·cm | = (1011 c−2) s |
| capacitance | C | 1 F | = (10−9 c2) cm | = (10-9) abF | = (10-9 c2) cm |
| inductance | L | 1 H | = (109 c−2) cm−1·s−2 | = (109) abH | = (109 c−2) cm−1·s2 |
In this table, c = 29,979,245,800 ≈ 3·1010 is the speed of light in vacuum in the CGS units of cm/s.
One can think of the SI value of the Coulomb constant kC as:
This explains why SI to ESU conversions involving factors of c2 lead to significant simplifications of the ESU units, such as 1 statF = 1 cm and 1 statΩ = 1 s/cm: this is the consequence of the fact that in ESU system kC=1. For example, a centimetre of capacitance is the capacitance between a sphere of radius 1 cm in vacuum and infinity. The capacitance C between two concentric spheres of radii R and r in ESU CGS system is:
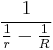 .
.
By taking the limit as R goes to infinity we see C equals r.
Physical constants in CGS units
| Constant | Symbol | Value |
|---|---|---|
| Atomic mass unit | u | 1.660 538 782 × 10−24 g |
| Bohr magneton | μB | 9.274 009 15 × 10−21 erg/G (EMU, Gaussian) |
| 2.780 278 00 × 10−10 statA·cm2 (ESU) | ||
| Bohr radius | a0 | 5.291 772 0859 × 10−9 cm |
| Boltzmann constant | k | 1.380 6504 × 10−16 erg/K |
| Electron mass | me | 9.109 382 15 × 10−28 g |
| Elementary charge | e | 4.803 204 27 × 10−10 Fr (ESU, Gaussian) |
| 1.602 176 487 × 10−20 abC (EMU) | ||
| Fine-structure constant | α ≈ 1/137 | 7.297 352 570 × 10−3 |
| Gravitational constant | G | 6.674 28 × 10−8 cm3/(g·s2) |
| Planck constant | h | 6.626 068 85 × 10−27 erg·s |
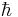 |
1.054 5716 × 10−27 erg·s | |
| Speed of light in vacuum | c | ≡ 2.997 924 58 × 1010 cm/s |
Pro and contra
While the absence of explicit prefactors in some CGS subsystems simplifies some theoretical calculations, it has the disadvantage that sometimes the units in CGS are hard to define through experiment. Also, lack of unique unit names leads to a great confusion: thus “15 emu” may mean either 15 abvolt, or 15 emu units of electric dipole moment, or 15 emu units of magnetic susceptibility, sometimes (but not always) per gram or per mole. On the other hand, SI starts with a unit of current, the ampere, which is easier to determine through experiment, but which requires extra prefactors in the electromagnetic equations. With its system of unique named units, SI also removes any confusion in usage: 1 ampere is a fixed quantity of a specific variable, and so are 1 henry and 1 ohm.
A key virtue of the Gaussian CGS system is that electric and magnetic fields have the same units, 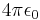 is replaced by
is replaced by 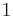 , and the only dimensional constant appearing in the equations is
, and the only dimensional constant appearing in the equations is  , the speed of light. The Heaviside–Lorentz system has these desirable properties as well (with
, the speed of light. The Heaviside–Lorentz system has these desirable properties as well (with 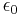 equaling 1), but it is a "rationalized" system (as is SI) in which the charges and fields are defined in such a way that there are many fewer factors of
equaling 1), but it is a "rationalized" system (as is SI) in which the charges and fields are defined in such a way that there are many fewer factors of 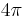 appearing in the formulas, and it is in Heaviside–Lorentz units that the Maxwell equations take their simplest form.
appearing in the formulas, and it is in Heaviside–Lorentz units that the Maxwell equations take their simplest form.
In SI, and other rationalized systems (for example, Heaviside–Lorentz), the unit of current was chosen such that electromagnetic equations concerning charged spheres contain 4π, those concerning coils of current and straight wires contain 2π and those dealing with charged surfaces lack π entirely, which was the most convenient choice for electrical-engineering applications. In those fields where formulas concerning spheres dominate (for example, astronomy), it has been argued that the non-rationalized CGS system can be somewhat more convenient notationally.
In fact, in certain fields, specialized unit systems are used to simplify formulas even further than either SI or CGS, by using some system of natural units. For example, the particle physics community uses a system where every quantity is expressed by only one unit, the eV, with lengths, times, and so on. all converted into eV's by inserting factors of c and 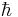 . This unit system is very convenient for particle-physics calculations, but would be impractical in other contexts.
. This unit system is very convenient for particle-physics calculations, but would be impractical in other contexts.
See also
- List of scientific units named after people
- SI electromagnetism units
- International System of Units
- Units of measurement
References and notes
- ^ Hallock, William; Wade, Herbert Treadwell (1906). Outlines of the evolution of weights and measures and the metric system. New York: The Macmillan Co. p. 200. http://books.google.com/?id=NVZKAAAAMAAJ.
- ^ For historical reasons, 1 ampere is chosen such that the magnetic force exerted by two infinitely long, thin, parallel wires 1 m apart and carrying this current is exactly 2×10–7 N/m. This definition makes all SI electromagnetic units consistent (up to some integer powers of 10) with the EMU CGS system described in further sections.
- ^ a b c d e f g h Jackson, John David (1999). Classical Electrodynamics (3rd ed.). New York: Wiley. pp. 775–784. ISBN 0-471-30932-X.
- ^ Cardarelli, F. (2004). Encyclopaedia of Scientific Units, Weights and Measures: Their SI Equivalences and Origins (2nd ed.). Springer. p. 20. ISBN 1-8523-3682-X. http://books.google.com/?id=6KCx8Ww75VkC.
- ^ a b Leung, P. T. (2004). "A note on the 'system-free' expressions of Maxwell's equations". European Journal of Physics 25 (2): N1–N4. doi:10.1088/0143-0807/25/2/N01.
- ^ a b c d e f Cardarelli, F. (2004). Encyclopaedia of Scientific Units, Weights and Measures: Their SI Equivalences and Origins (2nd ed.). Springer. pp. 20–25. ISBN 1-8523-3682-X. http://books.google.com/?id=6KCx8Ww75VkC.
- ^ Bennett, L. H.; Page, C. H.; and Swartzendruber, L. J. (1978). "Comments on units in magnetism". Journal of Research of the National Bureau of Standards 83 (1): 9–12.
- ^ A.P. French, Edwind F. Taylor (1978). An Introduction to Quantum Physics. W.W. Norton & Company.
General literature
- Griffiths, David J. (1999). "Appendix C: Units". Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Jackson, John D. (1999). "Appendix on Units and Dimensions". Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X.
- Littlejohn, Robert (Fall 2007). "Gaussian, SI and Other Systems of Units in Electromagnetic Theory" (PDF). Physics 221A, University of California, Berkeley lecture notes. http://bohr.physics.berkeley.edu/classes/221/0708/notes/emunits.pdf. Retrieved 2008-05-06.
|
||||||||||||||||||||